Going Elliptic on TLS-certificates

The TLS-certificate for this blog was up for expiration. As I'm always eager to investigate TLS and test things, I'm doing an experiment of my own and went for more modern stuff. Also I've been wanting to obsolete TLS versions 1 and 1.1, so I went for an Elliptic-Curve private key. If you can read this, you probably operate reasonable modern hardware, operating system and browser. If you for some reason stop to see my writings, then you're out of luck. I don't support your obsoleted stuff anymore!

Here are the old and new certs side-by-side:

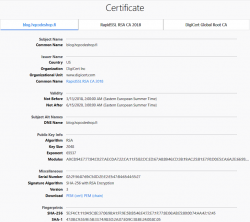
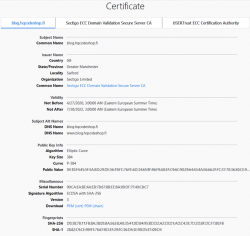
Obvious differences are:

• Expiry: 2+ years of lifetime left. Note: They sold the cert as a 5 year one, but I know about Apple's recent decision to shorten the lifetime of a TLS-cert. Read all about it from About upcoming limits on trusted certificates.
• Issuer: Sectigo ECC Domain Validation Secure Server CA, RapidSSL/DigiCert won't issue ECDSA on cheap certs
• Certificate chain: ECDSA and SHA-2 256-bits on certificate, intermediate-CA and root-CA
• Key-pair type: Now there is a 384-bit secp384r1 curve instead of plain-old-RSA

If you want, you can do almost the same with Let's Encrypt. Getting an ECDSA-cert out of Let's E used to be a tedious manual task, but I'm using acme.sh for my LEing. Its readme says:

Let's Encrypt can now issue ECDSA certificates.
And we support them too!
Just set the keylength parameter with a prefix ec-.

Example command to get a 384-bit ECDSA certificate from Let's Encrypt with acme.sh:

$ ./acme.sh --issue --dns dns_rackspace --keylength ec-384 -d example.com

That's no different than getting a RSA-certificate. The obvious difference in Let's Encrypt cert and my paid cert is in the certificate chain. In Let's E, chain's CA-types won't change from RSA, but your own cert will have elliptic-curve math in it.

Note:
Some people say ECDSA is more secure (example: ECC is faster and more secure than RSA. Here's where you (still) can't use it). ECDSA is modern and faster than RSA, that's for sure. But about security there is controversy. If you read Wikipedia article Elliptic-curve cryptography - Quantum computing attacks, there is note: "... suggesting that ECC is an easier target for quantum computers than RSA". There exists a theory, that a quantum computer might be able to crack your curve-math easier than your prime math. We don't know if that's true yet.